O problema urbanístico que deu origem à teoria dos grafos
Leonard Euler queria cruzar as sete pontes de Königsberg, sem repetir nenhuma. Não conseguiu – mas criou uma das principais áreas da matemática.

A cidade de Königsberg, na antiga Prússia, é uma daquelas preciosidades históricas: foi casa de Immanuel Kant, Hannah Arendt, E. T. A. Hoffmann, Christian Goldbach (o da conjectura) e vários outros cientistas e filósofos. Você não vai encontrá-la nos mapas, já que o município foi anexado à Rússia e mudou de nome para Kaliningrado. Mas, no século 18 e 19, Königsberg abrigava as mentes mais brilhantes da época.
A região é cruzada pelo rio Prególia, o que cria duas ilhas na cidade. Cada uma delas é conectada às duas margens do rio e entre si por sete pontes. Veja no mapa abaixo.
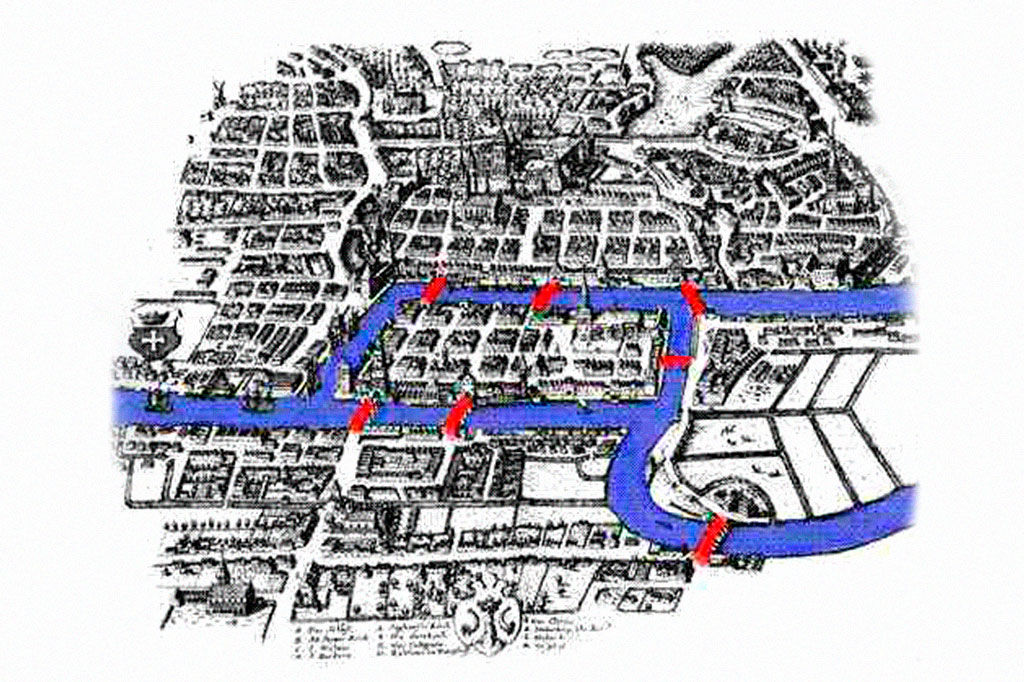
Kant ficou famoso por sua rotina pontual: todos os dias, fazia sua caminhada pela cidade precisamente às 15h30. Outra pessoa que curtia essas andanças era o matemático Carl Gottlieb Ehler, só que com um detalhe: ele passava horas imaginando qual rota deveria fazer para cruzar todas as pontes, sem repetir nenhuma delas.
Você pode tentar encontrar a solução – mas vai desistir em breve, porque a tal rota não existe. O problema ocupava tanto a mente do matemático que ele escreveu uma carta ao colega Leonhard Euler sobre a questão. Euler inicialmente achou que o problema não tinha a ver com matemática, mas logo percebeu que estava errado.
Ao explicar por que cruzar as sete pontes uma única vez seria impossível, Euler criou um novo campo da matemática, chamado por ele de “geometria das posições”. Hoje, o conhecemos por teoria dos grafos.
O matemático simplificou o mapa, representando cada ilha e margem por um ponto. As pontes, por sua vez, viraram apenas linhas, resultando em um desenho parecido com este:
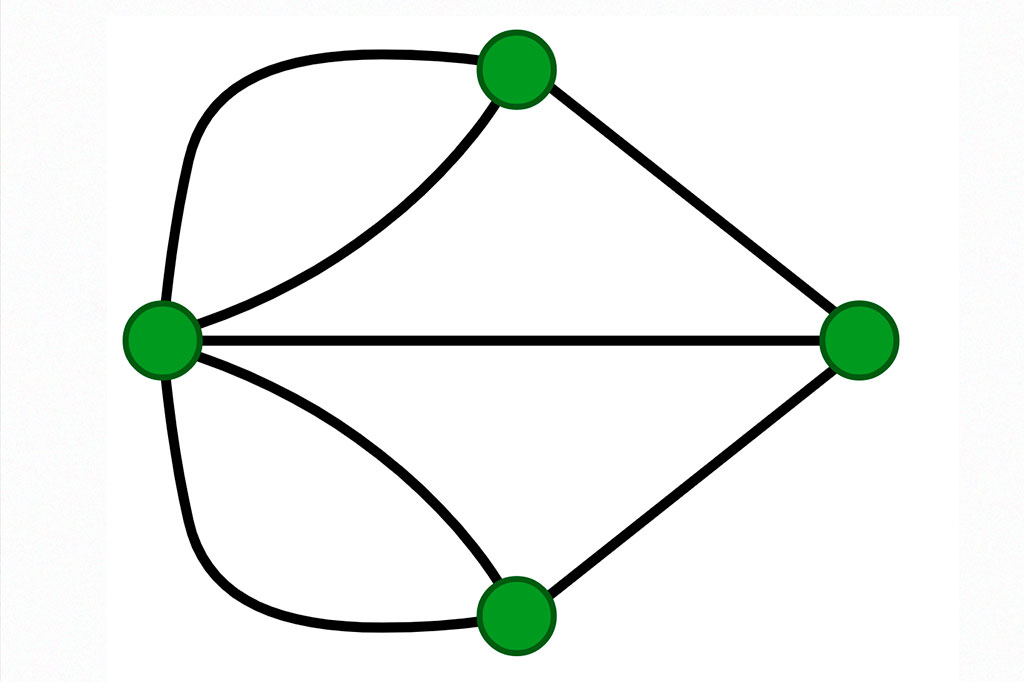
Dessa forma, conseguimos visualizar melhor quantas linhas saem de cada ponto (que hoje chamamos de “vértice”). Pensa só: para atravessar uma ilha, o transeunte deve entrar e sair dela por pontes distintas. Portanto, cada ilha deveria ter um número par de pontes – as de “entrada” e as de “saída”. As únicas exceções seriam as ilhas onde a caminhada inicia e termina. Essas podem ter um número ímpar de pontes.
Pensando dessa forma, é fácil perceber que todos os quatro pontos do desenho (que chamamos de grafo) são conectados por um número ímpar de linhas. Portanto, não há como fazer a caminhada sem repetir pelo menos uma delas em algum momento.
Se todos os pontos tivessem um número par de linhas, então seria possível sair e voltar à mesma ilha sem repetir nenhuma ponte – algo que chamamos de circuito euleriano.
Leonhard Euler provou isso em 1736, em um artigo que é considerado o início da teoria dos grafos. Hoje, usamos grafos para estudar e visualizar diferentes tipos de relações – em uma malha metroviária ou entre links na internet, por exemplo.
Em agosto de 1944, durante a Segunda Guerra Mundial, duas das pontes originais foram bombardeadas pela força aérea soviética. Se Ehler e Euler estivessem vivos na época, poderiam fazer a tão desejada caminhada pelas pontes sem repetir nenhuma delas (após o final da guerra, é claro).













